断层侧向封闭评价方法

岩性对接评价方法

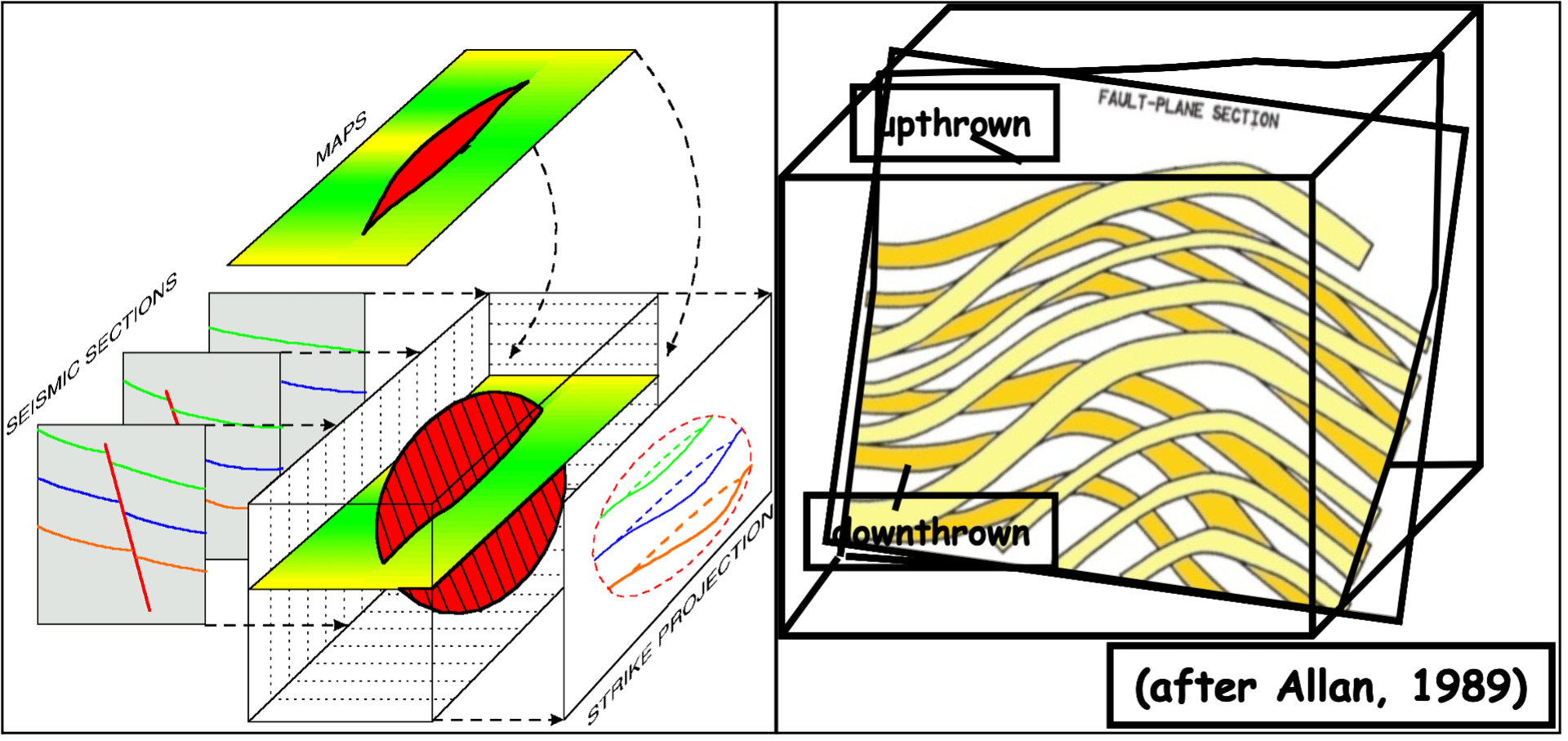
Allan图

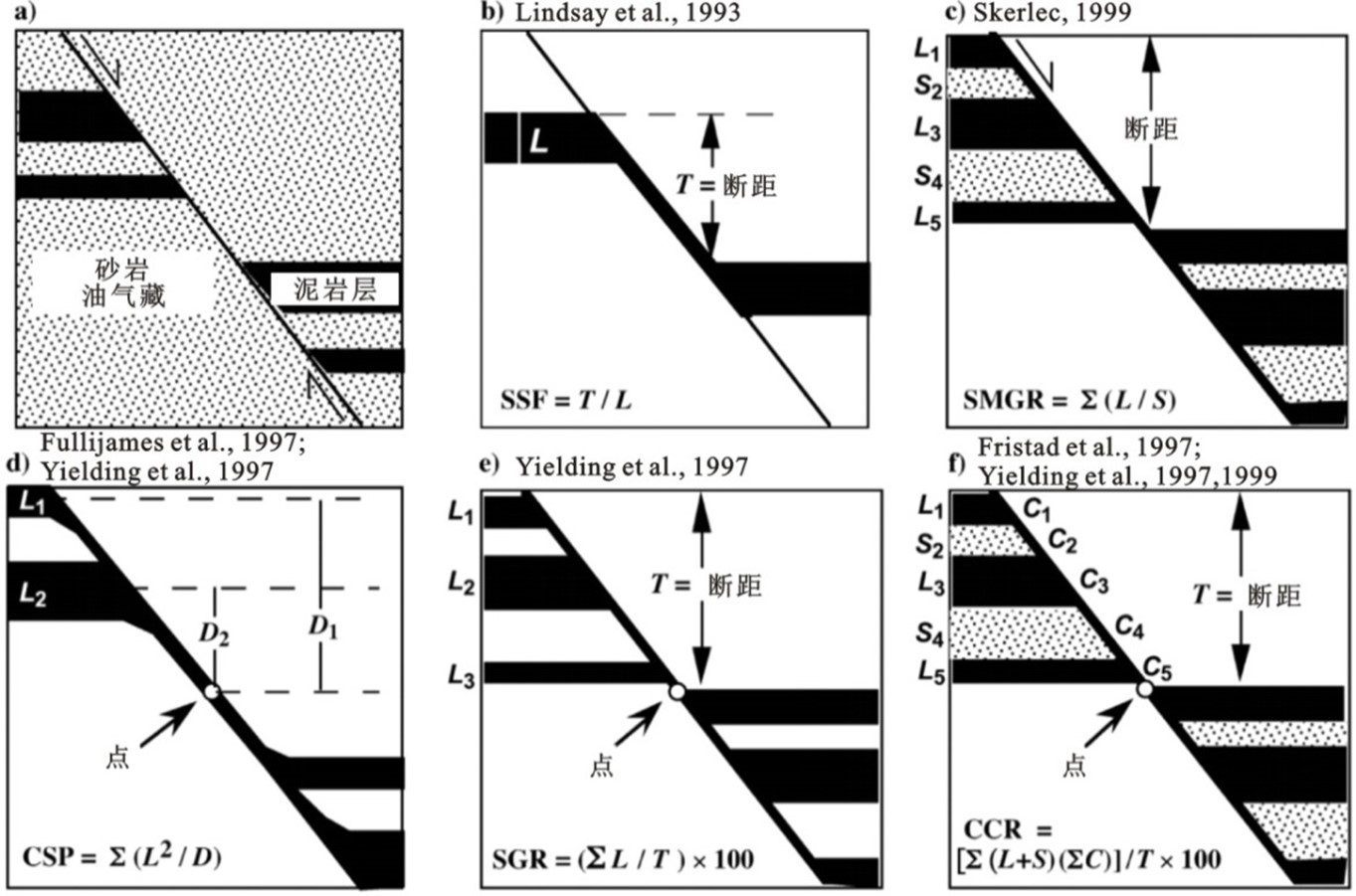
Allan（1989）建立了对接封闭的评价模型，通过断层两侧岩层厚度、地层形态、岩性与断距大小之间的关系提出了断层面岩性对接图—Allan图，直观地反映了断层面任意位置的岩性对接状况，并认为砂岩和泥岩对接能够形成有效的侧向封闭条件，而砂岩和砂岩对接为侧向渗漏。

利用Allan和Knipe定性评价断层侧向封闭性原理及方法断层错断岩层时，沿断层走向断距是变化的：断裂中心断距最大，向两侧逐渐减为零。我们可以依据地震解释数据中断层断距的变化及断层两侧岩性关系，将上下盘同时投影到断层面上，就形成了Allan图。

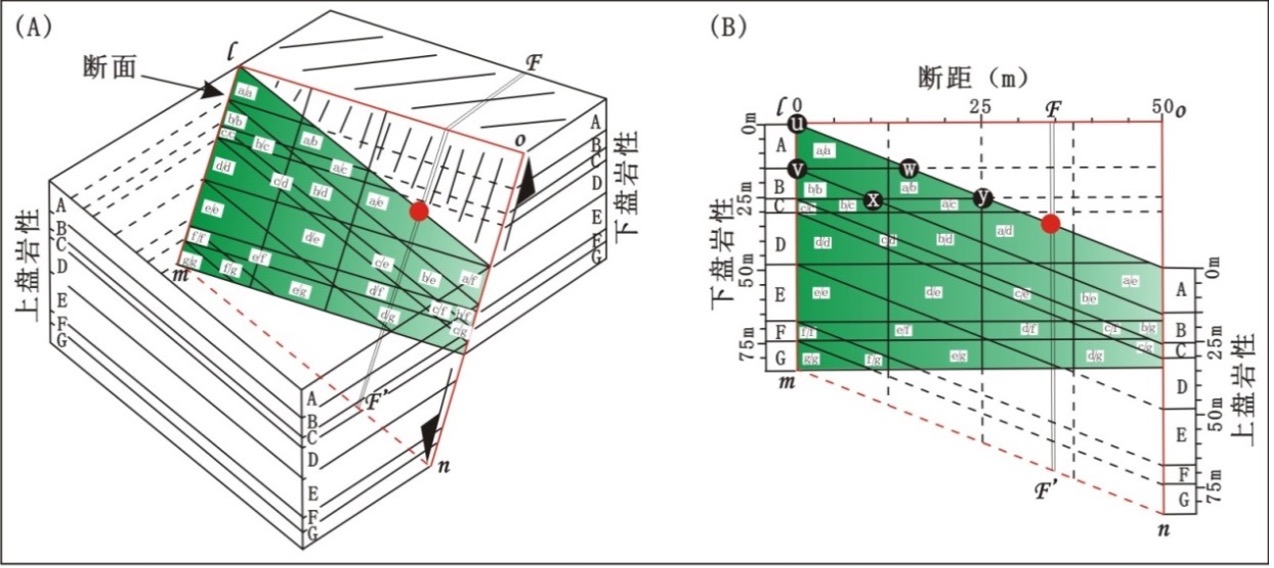
三角图（Knipe图）

Knipe(1997)(1)采用了三角图方式（或称Knipe图）表征断层两盘岩性对接关系，该图以钻井资料为基础，以井为单位，利用泥质含量曲线区分砂岩与泥岩，并把这些小层做为编制Knipe图解的基本单元。依据岩性划分结果，编制Knipe图解岩性对接图。这种图件无需作水平地层和断层面的三维图便可成图，能够迅速清晰展示不同断距下断层两盘的岩性对接关系，可用于评价正断层或逆断层的封闭性，即断层两盘地层厚度和层序无明显变化的断层。

1. KNIPE, R.J., 1997: Juxtaposition and seal diagrams to help analyze fault seals in hydrocarbon reservoirs, AAPG Bulletin, 81, 187-195.

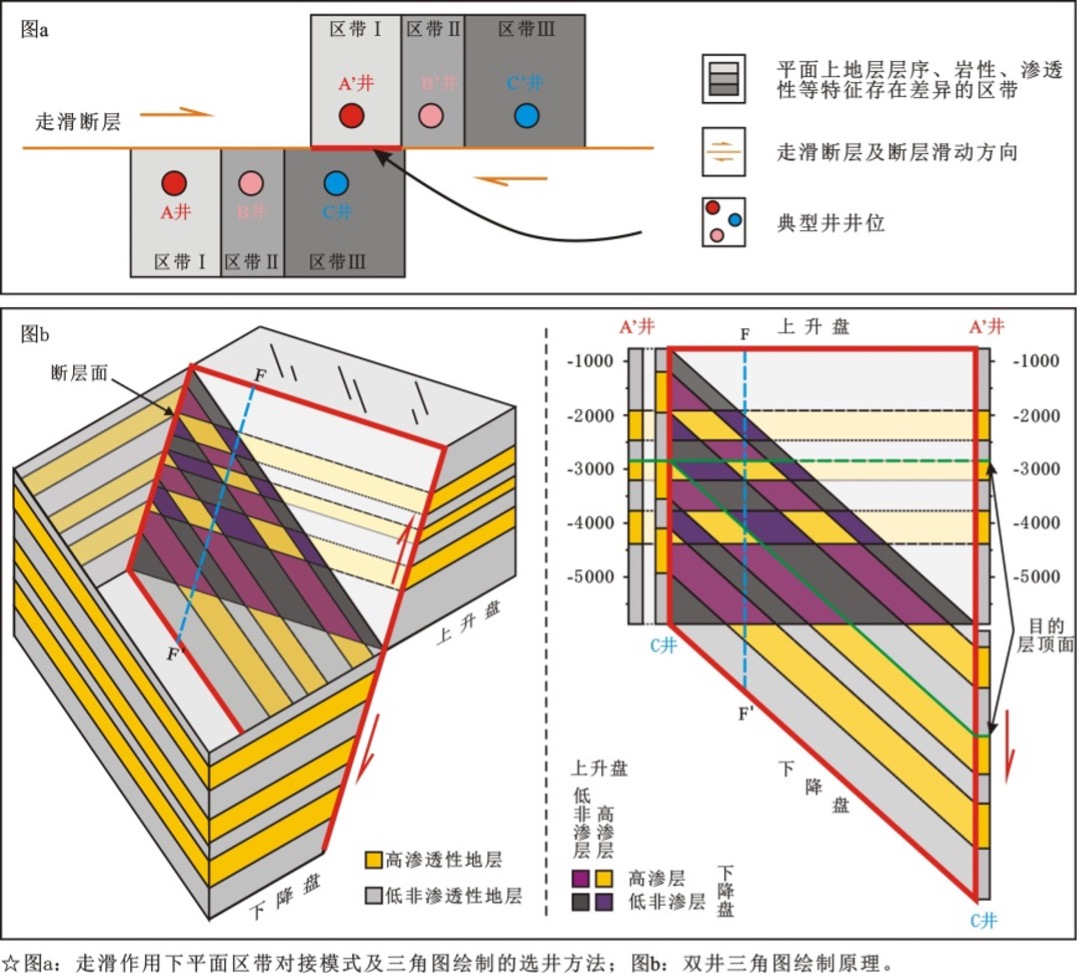
对于走滑断层的评价，孟令东（2014）提出了“双井三角图”方法，该方法进一步弥补了对走滑断层两盘岩性对接关系的表征

断层岩封闭能力评价方法

基于断层泥含量的评价方法

静水条件下断层封闭能力强弱依赖于断层与储层的排替压力差的大小，Gibson（1994）经实验研究证实，泥质中的细粒物质可有效降低断层岩的孔隙度，从而起到增加断层带毛细管力的作用，故泥质含量越大断层的封闭能力越强。Yileding（1997）在对尼日尔三角洲的那恩河油田的断层封闭性研究过程中发现，无论使用哪一种参数表征断层带中泥质含量的多少，过断层压力差都随泥质含量增加而增加。因此如何准确地预测断层带中的泥质含量，并建立泥质含量与过断层压力差之间的关系，成为断层封闭性评价的首要任务。

多位学者依据露头数据和实验室研究，先后提出了多套预测断层带泥质含量的计算方法：

泥岩涂抹因子（SSF）

Lindsay等人（1993）(1)引入了泥岩涂抹因子（SSF）来计算夹带到断层岩中泥质含量，单层泥岩的SSF定义为断层断距\(T\)除以原岩层厚度\(L\)：

1. Lindsay, N.G., Murphy, F.C., Walsh, J.J. and Watterson, J. (1992). Outcrop Studies of Shale Smears on Fault Surface. In The Geological Modelling of Hydrocarbon Reservoirs and Outcrop Analogues (eds S.S. Flint and I.D. Bryant). https://doi.org/10.1002/9781444303957.ch6

\[ SSF={T\over L} \]

提示

SSF本身只适用于单层，两层及以上泥岩的SSF值则采用SGR的倒数：

\[ SSF={1\over SGR} \]

断层泥比率（SGR）

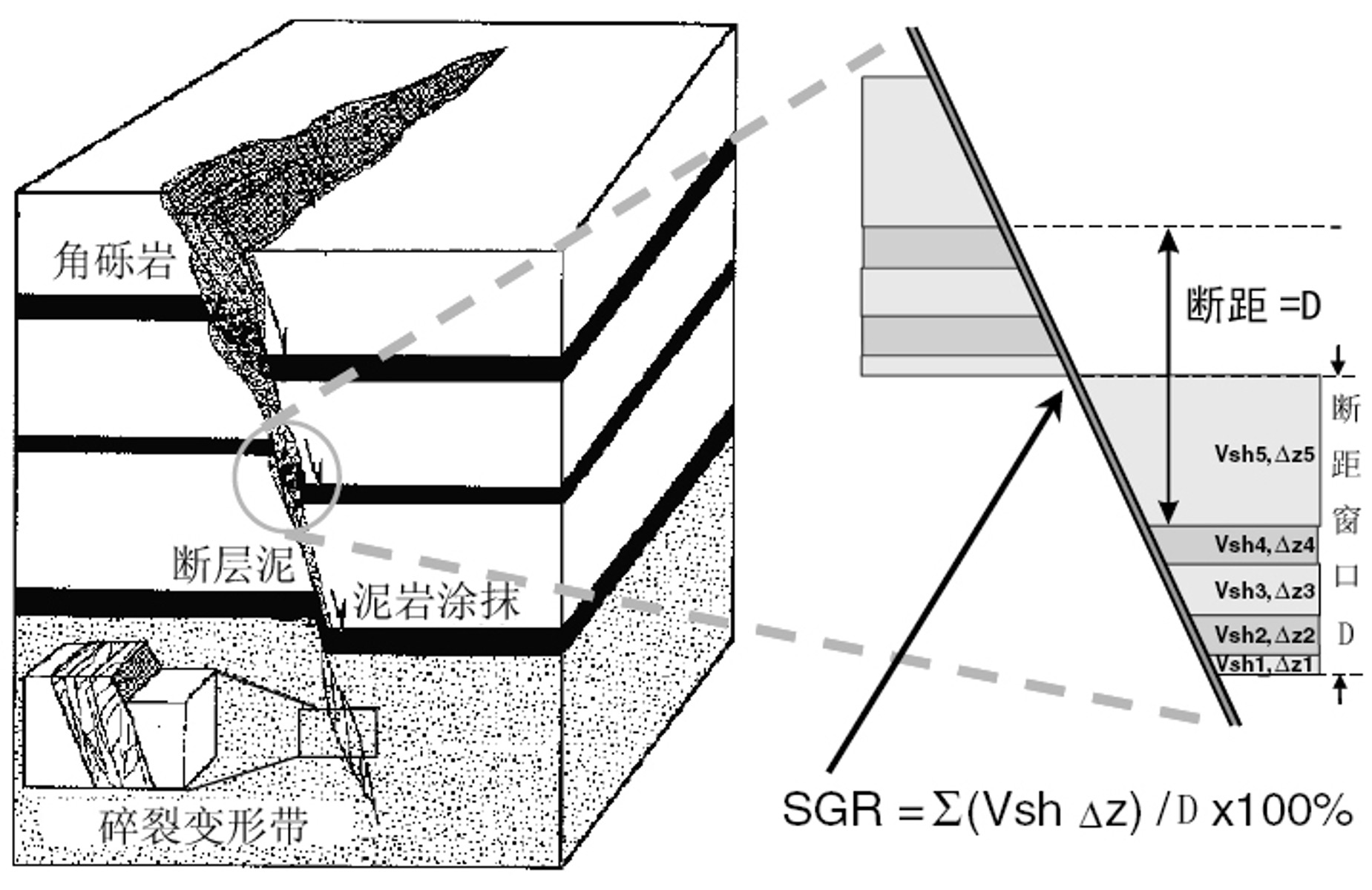
Yielding（1997）(1)提出了SGR（Shale Gouge Ratio，断层泥比率），即断层带内某一点的泥质含量，其值为被错断地层划过该点的累积泥岩厚度与该点断距的比值，SGR是目前应用最为广泛的计算方法：

1. Yielding, Graham, B. Freeman and D. T. Needham.“Quantitative Fault Seal Prediction” AAPG Bulletin 81 (1997): 897-917. DOI:10.22587/ajbas.2019.13.9.1

\[ SGR={\varSigma(V_{sh}*\Delta Z) \over D}*100\% \]

式中：\(\Delta Z\)——地层厚度(m)，\(V_{sh}\)——地层的泥质含量(%)，\(D\)——断距(m)。

使用SGR时，设定泥岩层为100%泥岩，非泥岩层为0%泥岩，在FAPSeal中，判断是否为泥岩是通过该处的VSH曲线是否超过设定的泥岩比来控制的。

过断层压力差 (AFPD)

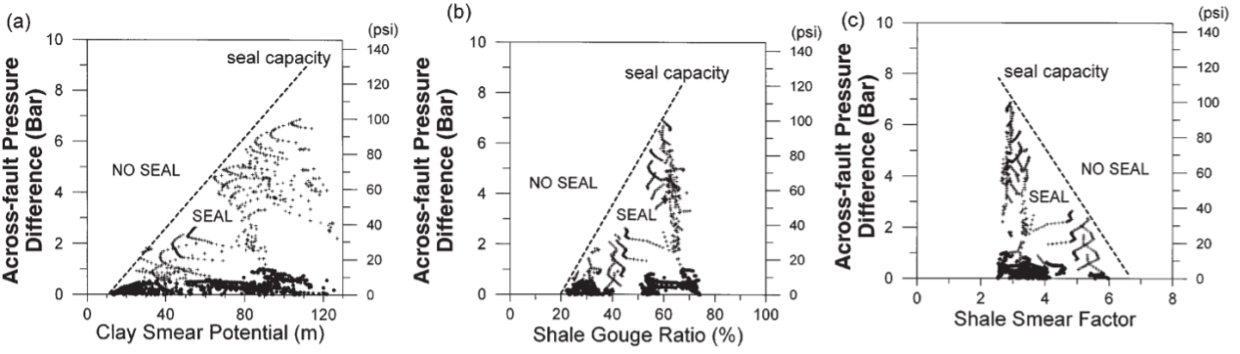
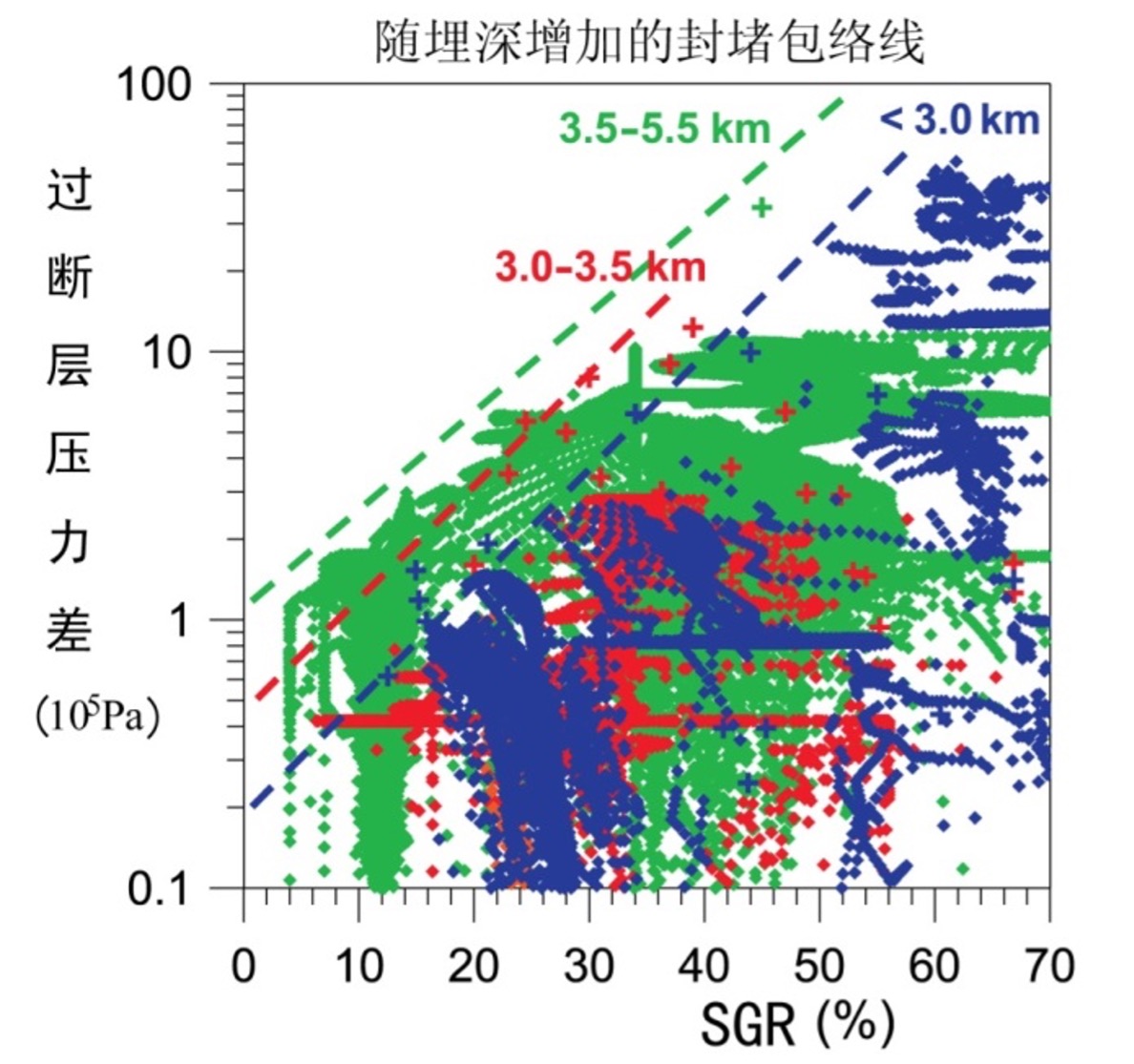
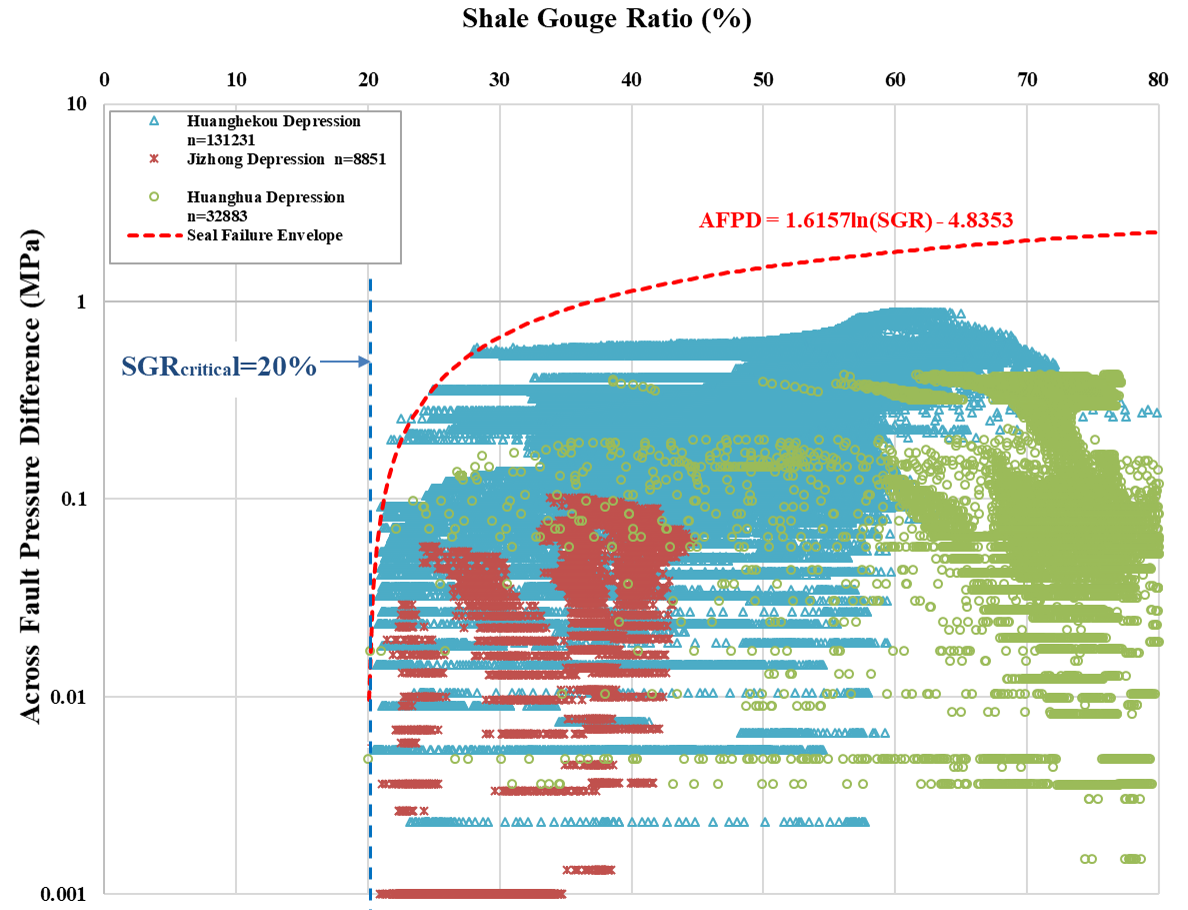
Yielding（1997）(1)对多个盆地中断层带SGR与过断层压力差数据进行了统计，得出在不同深度下存在着不同的AFPD-SGR有效封闭包络线，如下图所示：

1. Bretan, P., Yielding, G., & Jones, H. (2003). Using calibrated shale gouge ratio to estimate hydrocarbon column heights. AAPG Bulletin, 87(3), 397–413. doi:10.1306/08010201128

并建立了该包络线方程：

\[ AFPD=10^{({SGR \over D}-c)} \]

式中：C为与深度相关的常数，埋深小于3000m时，C=0.5，埋深在3000~3500m之间时，C=0.25，埋深超过3500km时，C=0。

由过断层压差AFPD与其所能支撑的烃柱高度H的对应关系：

\[ H={AFPD \over (\rho_w-\rho_o)g} \]

以及上述的AFPD-SGR有效封闭包络线方程，即可得出SGR与其所能支撑烃柱高度的关系：

\[ H={10^{({SGR \over D}-c)} \over (\rho_w-\rho_o)g} \]

式中：H——断层面某点支撑的烃柱高度（m）；SGR——断层面某点泥质含量（0～100）；d——变量（介于0～200），不同地层不同层位取值不同，通过调整d值及对应的SGR临界值，使预测的气水界面与实际的气藏气水界面吻合；ρw——气藏中水的密度（g/cm³）；ρo为——气藏中气的密度（g/cm³）；g——重力加速度（m/s²）。

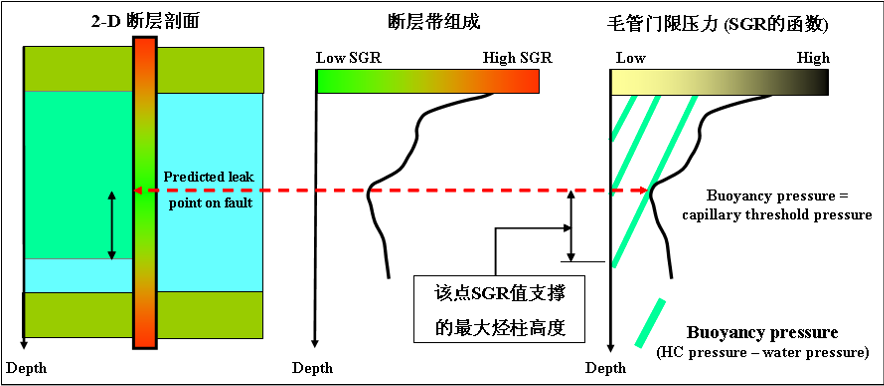
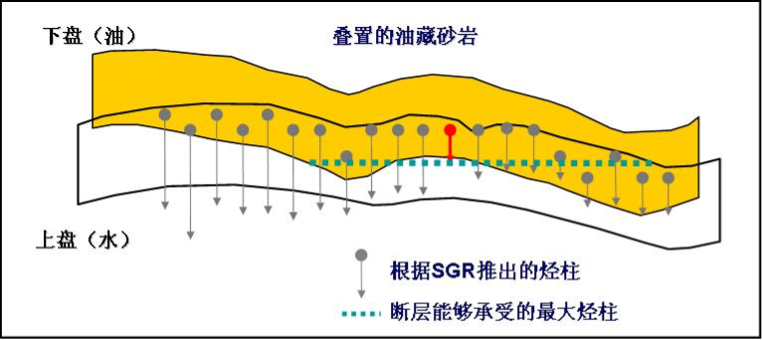
三维空间断层面形态和断裂带填充物均为非均质体，断裂带内任何一点的SGR值都是不同的，由此对应的断裂带毛细管门限压力（SGR的函数）大小不一，随着油气不断向断层圈闭内充注，浮压越来越大，当浮压与断裂带最小的毛细管门限压力相等时，断裂带开始侧向渗漏，如下图所示。

因此最小毛细管门限压力决定一个圈闭气水界面的深浅。

断层渗透率

Manzocchi等人（1999）(1)通过开展对野外露头、实际油藏断层核岩心的渗透率测试实验，在其实验基础上，并将泥岩体积分数（\(V_f\)）和渗透率（\(k_f\)）联系起来。在下面的经验方程中，他们从\(SGR\)推导出了\(V_f\)。此外，他们还整合了一个有关位移的因子（\(D\)），该因子用于解释碎裂作用导致的渗透率降低。

1. Manzocchi T, Walsh J J, Nell P. Fault transmissibility multipliers for flow simulation models[J]. Petroleum Geoscience, 1999, 5(1): 53–63. (https://doi.org/10.1144/petgeo.5.1.53)

\[ logk_f=-4SGR-{1\over4}\log(D)(1-SGR)^5 \]

Sperrevik等（2002）(1)提出在综合了碎裂作用、压实作用和成岩/胶结作用等因素的影响，\(k_f\)更取决于最大埋深\(Z_{max}\)和断裂时的深度\(Z_f\)。利用一组从断层核岩心试验中测量中获得的\(V_f\)与渗透率数据，他们提出了以下经验关系式:

1. Sperrevik, S., Gillespie, P. A., Fisher, Q. J., Halvorsen, T., & Knipe, R. J. (2002). Empirical estimation of fault rock properties. Hydrocarbon Seal Quantification, Norwegian Petroleum Society Conference, 109–125. doi:10.1016/s0928-8937(02)80010-8

\[ k_f=a_1exp\left\{-\left[a_2V_f+a_3z_{max}+\left(a_4z_f-a_5\right)\left(1-V_f\right)^7\right]\right\} \]

常数如下: \(a_1\)=80,000; \(a_2\)=19.4; \(a_3\)=0.00403; \(a_4\)=0.0055; \(a_5\)=12.5。同一数据集还得到了断层岩渗透率与毛管临界压力（\(P_f\)）的经验关系。

\[ P_f=31.838\times\ k_f^{-0.3848} \]

传导因子

在油藏模拟中，断层并不需要详细地建模，而是作为模型单元之间的连接。这种连接没有厚度，这是物理上正确计算断层通量所必需的。因此，断层的特性，如渗透率，在模拟中作为被断层分开的单元接触处的乘法因子。这些乘法因子可对一些特性进行校正，比如从一个单元到另一个单元的流量。这些被称为断层的传导因子（FTM或T）（Manzocchi等人，1999）。定义两个模型单元i和j之间的传导因子T为：

\[ T=\left[1+t_f\frac{\left(\frac{2}{k_f}-\frac{1}{k_i}-\frac{1}{k_j}\right)}{\left(\frac{L_i}{k_i}+\frac{L_j}{k_j}\right)}\right]^{-1} \]

式中\(T\):传导因子；\(t_f\):断层带厚度；\(k_f\)：断层渗透率；\(k_i\)、\(k_j\)：i、j网格中母岩渗透率；\(L_i\)、\(L_j\)：i、j网格长度。

断层岩或断层带厚度，作为等式（FTM）中的输入参数，是岩性和断层位移的函数，并且相关性较强（Torabi和Berg, 2011）。一般来说，可以假定富黏土层中的断层核要比砂岩中的断层核要窄。基于这一假设，Sperrevik et al.（2002）为此建立了一个经验公式来计算断层带厚度（F）：

\[ F=T\left(0.06V_f^2-0.12V_f+0.0659\right) \]

式中\(T\)：断距；\(V_f\)：断层岩中的泥岩体积，来源于SGR。

断接厚度(CJT)

断裂对盖层的破坏程度主要取决于断裂的断距和盖层厚度的相对大小，如果断裂断距大于有效盖层厚度，盖层被断裂完全错断，盖层完整性被破坏，就会失去封闭能力，如果断裂断距小于有效的盖层厚度，断裂虽然切割了盖层，但仍有一部分盖层横向保持连续，可以封闭一定高度的烃柱，因此提出了断接厚度（CJT）的概念，用以计算盖层被断裂破坏的程度：

\[ CJT={MT-T\over MT} \]

式中：CJT为断接厚度，MT为盖层厚度(m)，T为断裂断距(m)。CJT越大，表明残余的有效盖层厚度越大，盖层被破坏的程度越小，盖层的封闭能力越强。

基于多维封闭性因素的评价方法

近些年，基于几十年的断层封闭性基础研究成果，部分学者尝试将机器学习算法融入到断层封闭性评价方法中，以实现基于多因素分析的断层封闭能力评价：

蒙特卡洛模型可以用来模拟断层对圈闭影响，可以显示出断层封闭性、断层方位、区域应力张量和圈闭几何形状对油气形成的影响。蒙特卡洛模型可以将问题简化为一维分析，通过模拟断层对接和断层封闭以及水动力效应和断层复活风险等一系列因素，预测断层圈闭烃柱高度，最终对圈闭油藏潜力进行预测。

Edmundson为提高油气柱高度预测的准确性，应用决策树算法预测断层圈闭充满程度，利用烃柱高度、圈闭高度和埋深数据计算了242口发现井的油气圈闭充填程度，将这些数据被聚合成一个简单的正演概率模型，根据埋深和圈闭高度计算出遇到不同范围圈闭的概率，发现圈闭充填比的分布与圈闭高度和埋深有明显的相关性。这些发现强烈表明，勘探区的尺寸和埋深或者其他的地下因素综合考虑，最终可以确定出最合适的钻前油气柱高度分布，标志着人们已经走出了人工智能在断层圈闭完整性评价中应用的第一步。

人工智能的方法可以将可以量化的数据应用到断层封闭性的评价当中去，但仍然存在一些无法量化的地质因素，例如早期断裂的埋藏时间、断层岩的成岩程度、断裂带的胶结充填作用等等，这些也是影响断层封闭性的重要因素，随着技术的进步，这些影响因素也会通过其他的方式考虑到断层封闭性评价模型当中去。

有关断层封闭性的影响因素，请参考断层岩封闭能力影响因素分析，此处列举了10种断层封闭性的影响因素

实例：基于BP神经网络的断层侧向评价模型

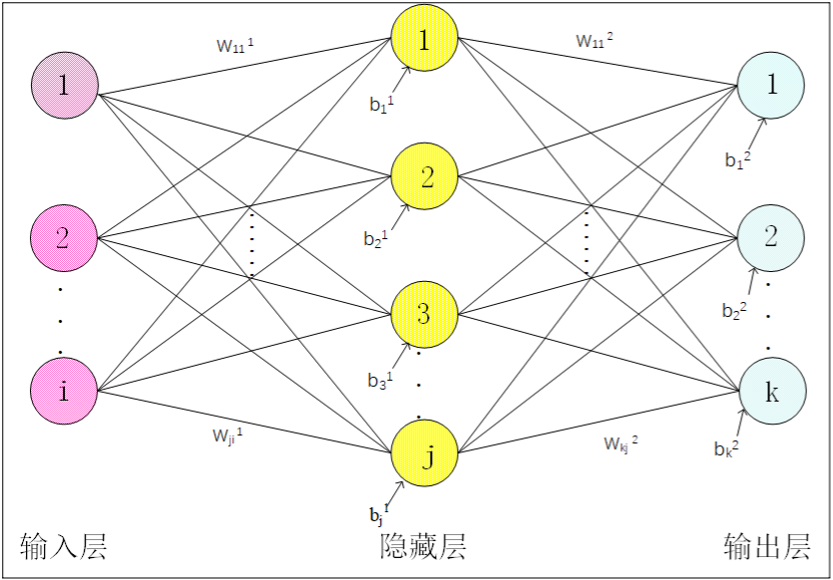
BP神经网络主要分为输入层、隐藏层、输出层，每层都有神经单元，输入层的神经单元就是为了读取输入的数据。隐藏层可以有多层，每层有多个神经单元。BP算法首先进行前向传播，输入的数据通过隐藏层进行矩阵乘法计算，然后输出到输入层。如果输出的数据与真实的数据不相符则进行反向传播，反向传播就是从输出层经过隐藏层到输入层，将前向传播的返回的误差分摊给隐藏层的各个神经单元，隐藏层的各个神经单元通过这个误差值调整矩阵计算中的参数使误差沿着梯度的方向进行下降，这样经过反复的训练，就会减少误差，当误差达到收敛即稳定时停止训练，从而完成BP评价模型的建立。

BP神经网络原理由连接权值分量和阈值构成了输入层与隐藏层各节点间、隐藏层与输出层各节点之间的关系。层之间的连接权重分量Wji1是与输入层的结点相乘的常量，而分层连接权值成分Wkj2是与隐藏层的结点相乘的常量，隐含层的结点具有bj1的阈值，而输出层的结点则具有bk2，通过权值的权值和权值的权重，再加上一个阈值，从而有效地减少了网络的调整。

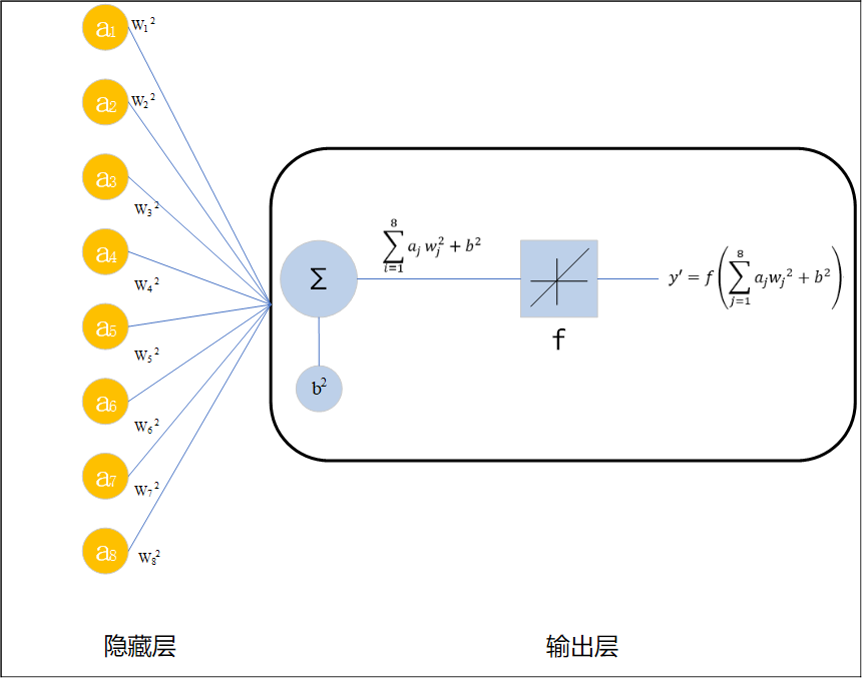
在特定的学习中，可以将其分成两大类：信号的正向传输和错误的逆向传输。选取70%的抽样进行人工神经网络的学习，首先对样本进行正方扩散运算。正向扩散如图所示：

在引入多个油柱最大高度的影响因子（i= l、2、...、n）后，采用BP算法的前向扩散，将输出预报的结果通过隐含层传送到输出层。隐含层的神经元转移功能是sigmoid类型，sigmoid关系式为：

\[ f(n)={1\over(1+e^{-n})} \]

式中：n——变量。

由此可得隐藏层输出值为\(a_j\)：

\[ a_j=f(\sum_{i=1}^{8}{x_i{w_{ji}}^1+bj^1)} \]

式中: \(a_j\)为隐藏层计算结果；\(x_i\)为输入层样本，即圈闭最大油柱高度影响因素；\({w_{ji}}^1\)为圈闭最大油柱高度影响因素与隐含层之间连接权值分量； \(bj^1\)为隐藏层节点阈值; \(i\)为圈闭最大油柱高度影响因素个数 \(j\)为隐藏层节点个数，j=1，2，3...

输出层的输出值计算公式为：

\[ y^{'}=f\left(\sum_{j=1}^{10}a_jw_j^2+b^2\right) \]

目标函数计算误差的公式：

\[ E=\sum_{q=1}^{Q}{E^q=\frac{1}{2}=\sum_{q=1}^{Q}\left(y^q-y^{q^\prime}\right)^2} \]

为了提升模型预测烃柱高度范围准确度与过拟合，引入学习步长η（η>0）,向误差减小的方向前进1个学习步长,得到输出层至隐藏层反向传递调整连接权值分量与阈值的公式为：

\[ \Delta w_j^2= -\eta{\frac{\partial{E}}{\partial{w_j^2}}}= -\eta{\frac{\partial{E}}{\partial{y'}}} \times{\frac{\partial{y'}}{\partial{w_j^2}}} =\eta(y-y')\times f\left (\sum^{10}_{j=1}a_jw_j^2+b^2\right) \]

\[ \Delta b^2= -\eta{\frac{\partial{E}}{\partial{b^2}}}= -\eta{\frac{\partial{E}}{\partial{y'}}} \times{\frac{\partial{y'}}{\partial{b^2}}} =\eta(y-y')\times f\left (\sum^{10}_{j=1}a_jw_j^2+b^2\right) \]

通过调整参数，使神经网络尽可能达到理想的结果。