跳转至

断层稳定性评价方法#

断层带强度通常比围岩弱，因此，根据与围岩的强度的差异、相对主应力的方向，原有的断层带可以被重新激活，而不是产生一个新的断层（例如，Jaeger等人，1976）。通过估算古应力场方位、大小、孔隙压力、断层岩强度和断层方位，可以确定断层再活化的相对概率。

基于对断层再活动机理和岩石破裂理论的认识，结合流体压力对断层形成及再活动的控制作用，许多学者提出了评价岩石破裂和断层再活动的方法，主要包括滑动趋势（Slip Tendency）、膨胀趋势（Dilation Tendency）、CFF（Coulomb Failure Function）、CPP（Critical Pressure Perturbation）和FAST（Fault AnalysisSeal Technology）方法等。

断层稳定性评价参数

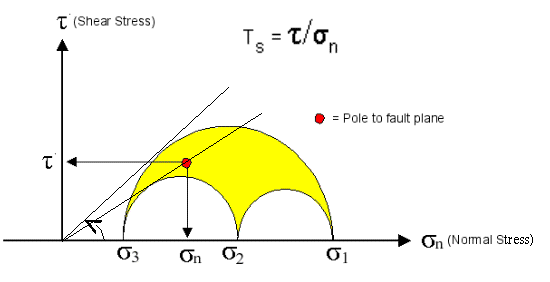
滑动趋势（Slip Tendency）#

Morris等人（1996）(1)提出了滑动趋势。滑动趋势为断层面剪切应力与有效正应力的比值，该比值介于0~μ（断层带摩擦系数）之间，用于描述无内聚力断层发生滑动（剪切破裂）趋势的强弱。 如图所示，当比值逐渐增大并趋近于静摩擦系数时，断层的滑动趋势逐渐增强，风险性升高，当超过静摩擦系数时，断层开始发生滑动。

  1. Alan Morris, David A. Ferrill, D.Brent Henderson; Slip-tendency analysis and fault reactivation. Geology 1996;; 24 (3): 275–278. doi: https://doi.org/10.1130/0091-7613(1996)024<0275:STAAFR>2.3.CO;2

滑动趋势原理图

\[ T_s={\tau}/{\sigma_n} \]

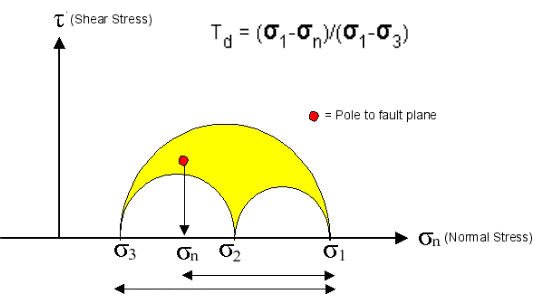
膨胀趋势（Dilation Tendency）#

Ferrill等人（1999）(1)在滑动趋势参数应用的基础上提出了膨胀趋势，并将其表征为最大主应力与断层所受正应力之差与差应力的比值:

  1. Ferrill, D.A., Winterle, J., Wittmeyer, G.W., Sims, D., Colton, S.L., & Armstrong, A. (1999). Stressed Rock Strains Groundwater at Yucca Mountain, Nevada. https://www.semanticscholar.org/paper/Stressed-Rock-Strains-Groundwater-at-Yucca-Nevada-Ferrill-Winterle/6713b04e8801b1bbaf069214548b83624ebec40a?utm_source=direct_link

裂缝的膨胀趋势为裂缝面所受正应力所控制。裂缝所受正应力取决于应力场和裂缝面的产状。裂缝发生膨胀和传输流体的能力与其孔径大小有着直接的关系，孔径大小是其所受有效正应力的函数。一个已知应力场中的任意平面所受正应力可以通过公式进行计算。将断层面所受正应力通过差应力进行正规化，即为最大主应力与断层所受正应力之差与差应力的比值。

因此膨胀趋势值介于 0~1 之间，随着趋势值增加，断层发生张性破裂的风险升高。

\[ T_d={{\sigma_1-\sigma_n}\over{\sigma_1-\sigma_3}} \]

膨胀趋势原理图

但该参数仅能定性表征断层发生张性破裂的相对趋势，也就是说膨胀趋势大于1时不能说明断层一定会发生张性破裂。从断层带强度模型研究得知，无内聚力的断层在发生张性破裂前就会以剪切破裂的形式发生滑动，因此该模型的应用更适合于对不同应力场下或不同产状的断层膨胀趋势进行对比分析。与滑动趋势相结合可以用来分析由地应力引起的渗透率的各向异性。

库仑破裂函数 CFF（Coulomb Failure Function）#

Castillo等人（2000）(1)对澳大利亚帝汶海断层稳定性研究中提出了库仑破裂函数。对于无内聚力的断层或者不考虑断层内聚力时，假设断层面开始滑动时其所受的有效正应力与摩擦系数乘积为断层发生滑动所需的临界剪切应力，CFF可以表征为无内聚力断面所受的实际剪切应力与临界剪切应力的差值，即断层发生滑动所需增加的最小剪切应力。

  1. Castillo, D. A., Bishop, D. J., Donaldson, I., Kuek, D., Ruig, M. de, Trupp, M., & Shuster, M. W. (2000). TRAP INTEGRITY IN THE LAM IN ARIA HIGH-NANCAR TROUGH REGION,TIMOR SEA: PREDICTION OF FAULT SEAL FAILURE USING WELL-CONSTRAINED STRESS TENSORS AND FAULT SURFACES INTERPRETED FROM 3D SEISMIC. The APPEA Journal, 40(1), 151–173. https://doi.org/10.1071/aj99009
\[ CFF=\tau-\mu(\sigma_n-P) \]

CFF为0Mpa时是断层活动的临界值，CFF＜0说明断层是稳定的，反之断层则发生再活动。由于断层面的剪切应力直接受控于地应力场和断层产状，因此该方法可用于对比和评价不同深度及相同深度下不同产状的断层滑动风险，但对于由流体压力变化引起的断层滑动风险则需要进一步换算。

临界压力扰动 CPP（Critical Pressure Perturbation）#

Wiprupt和Zoback(1)(2)于2002年提出了临界压力扰动(CPP)。CPP是无内聚力的断层发生滑动所需增加的最小流体压力值，该参数将滑动趋势的定性评价升级为定量表征。在已知地应力场和流体压力特征的情况下，应用CPP评价参数明确得出由流体压力变动所导致的断层滑动风险，对注水开发和天然气注气过程中注入压力的设定具有重要指导作用。

  1. Wiprut, D., & Zoback, M. D. (2000). Fault reactivation and fluid flow along a previously dormant normal fault in the northern North Sea.
  2. Wiprut, D., and M. D. Zoback, 2002, Fault reactivation, leakage potential, and hydrocarbon column heights in the northern North Sea, in A. G. Koestler and R. Hunsdale, eds., Hydrocarbon seal quantification: Norwegian Petroleum Society Special Publication 11, p. 17 – 35.

由于CPP不考虑内聚力，因此其在莫尔圆上的破裂包络线为一条穿过原点的直线。

CPP

临界压力扰动的最常用表征为滑动稳定性(Slip stability)，此外还有活化压力、活化压力系数等表征方法。

滑动稳定性 (Slip stability)#

滑动稳定性又称附加流体压力，表示在当前地层压力条件下还能额外承受的流体压力增量，用来识别断层的薄弱部位，其计算公式为：

\[P_p^{crit}=P_s=\Delta P=\sigma_n-\frac{\tau}{\mu}\]

活化压力#

活化压力为断层不发生活化所能承受的总上限压力，为滑动稳定性加入了当前深度的流体压力\(P_p\)，该参数常用于进行注水井注入压力的设计，其计算公式为：

\[P_r=\sigma_n-\frac{\tau}{\mu}+P_p\]

活化压力系数#

活化压力系数为断层发生活化所能承受的相对趋势，为滑活化压力与当前深度的流体压力之比，该参数对于描述不同深度下的断层稳定性很有帮助，其计算公式为：

\[P_{spc}={P_R\over P_f}\]

该参数一般为一个大于1的数值，比值越接近1，断层越容易发生滑动。

FAST（Fault Analysis Seal Technology）#

FAST方法是Mildren(1)在CPP参数的基础上，考虑了断层岩成岩作用所形成的断层带内聚力（CPP模型），因此在相同地质条件下，应用FAST方法对有内聚力的断层稳定性评价，得出的附加流体压力将大于CPP方法，与实际条件更加吻合。并且由于断层内聚力的作用，在差应力较小情况下可用来评价断层发生张性再活动的情形。

  1. Mildren, S. D., Hillis, R. R., Lyon, P. J., Meyer, J. J., Dewhurst, D. N., & Boult, P. J. (2005). FAST: A New Technique for Geomechanical Assessment of the Risk of Reactivation-related Breach of Fault Seals. 73–85. https://doi.org/10.1306/1060757H23163

其计算公式为：

\[P_{fast}=P_s+C\cot{\mu}=P_s+2T\cot{\mu}\]

其中C为岩石内聚力，T为岩石的抗张强度。