岩石破裂准则#
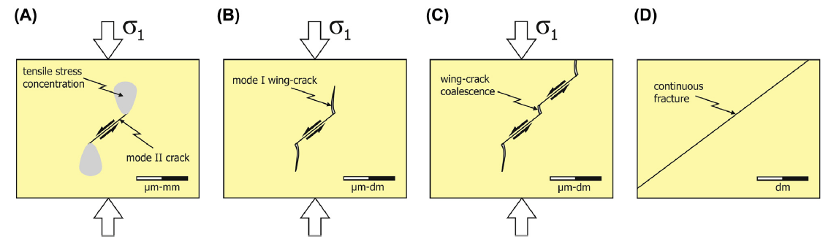
一般来说,断层的演化始于完整岩体中小规模张开型裂缝的发育,裂缝长度增加而后连接形成一个连续的剪裂缝。裂缝生长集中在裂缝末端。应力集中会导致所谓的翼破裂的形成。
任何岩石或甚至任何材料,无论是天然形成或人工制造的,都包含非常小的不连续裂缝,这些不连续裂缝可以成为裂缝形成的成核点。
格里菲斯破裂#
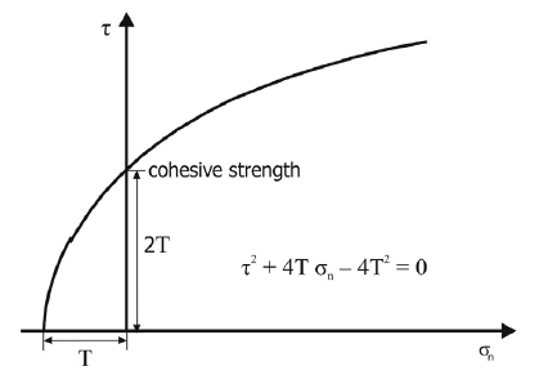
在20世纪初,A.A.Griffith分析了一个悖论,即材料的抗拉强度低于其理论内聚强度,而大多数材料的拉伸强度低于压缩强度,例如大块玻璃会在100MPa应力下断裂,而断裂玻璃原子键所需的的理论应力高达10GPa (Lawn, 1993)。格里菲斯发现材料抗张强度低是由于材料中存在微观结构的不连续性造成的(Griffith, 1921),这些微观不连续性现在被称之为“格里菲斯裂纹”,代表了晶格中的微观缺陷。
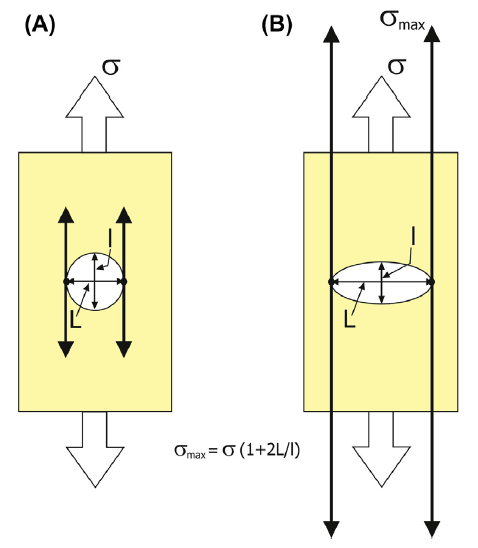
格里菲斯理论表明:应力增大取决于不连续面的纵横比。如果我们将格里菲斯裂纹看作是圆孔,那么在圆孔的边缘,应力将被放大三倍:在椭圆孔边缘的应力将会增加的更大。由于这种应力集中作用,局部张裂缝开始发育。裂纹末端的应力放大是裂纹生长的关键,取决于裂纹末端的方位、长度和曲率,从而导致某些裂纹优先生长(Brace, 1960)。在破幻之前,张裂缝的密度增加,随后裂缝愈合。这就会导致应变局部化和材料的宏观剪切破裂的形成(Hoek and Martin, 2014)。根据格里菲斯的研究,导致破裂所需的临界张应力取决于先存微裂纹的长度和裂缝传播过程中形成新的破裂面所需的能量;这就是现在所述的格里菲斯准则。作为近似值,岩石的抗张强度大约是理论值的五分之一。
库伦破裂准则与莫尔圆图解#
库伦破裂准则#
夏尔·奥古斯丁·库仑首次在18世纪提出了剪切破裂演化的基本概念(Coulomb, 1776)。在这个模型中,如果施加的外力超过材料的内聚力(c),且克服了沿着发展中的裂缝面的摩擦力,那么在完整岩石中就会形成剪切裂缝。这就称之为“库伦破裂准则”,其表示为:
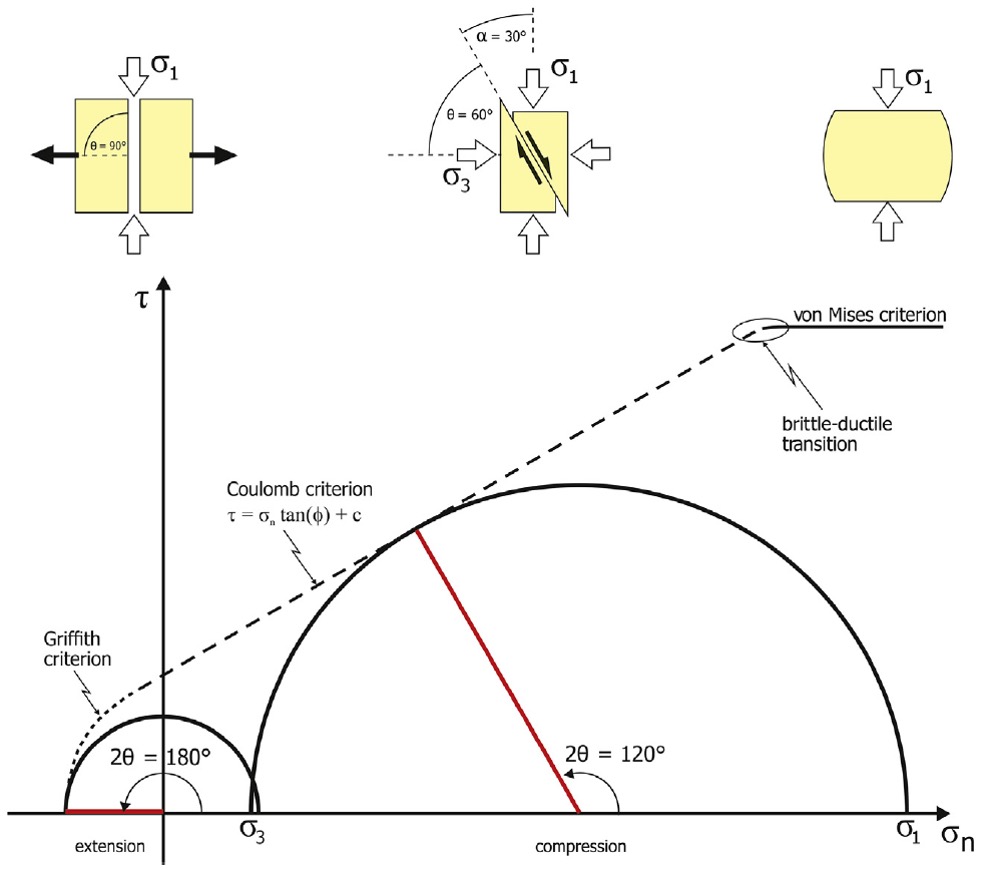
其中,\(C\)是内聚力,\(\phi\)是内摩擦角(取决于变形材料),\(\tau\)和\(\sigma_n\)是作用于裂缝面上的剪应力和正应力。如果内摩擦角是已知的,库伦破裂准则可以用于预测产生剪切裂缝所需应力。新生剪裂缝与最小主应力夹角为\(\theta\),其中大多数岩石\(\theta\)是60°,因此,剪裂缝与最大主应力夹角为30°(Ramsey and Chester, 2004)。
莫尔圆图解#
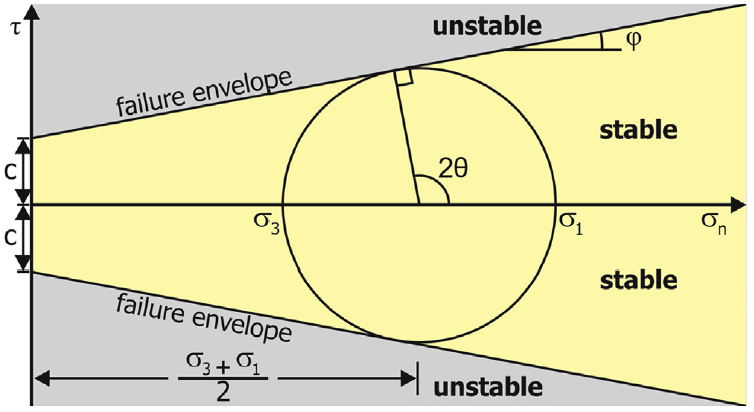
一种常见的可视化库伦破裂准则的方法是所谓的莫尔圆图解,由Mohr (1900)发展形成。莫尔圆是一种Cauchy应力张量变换定律的图形表示。因此,圆的周长代表施加在固体内任何定向面上的剪应力和正应力。
在莫尔圆中,剪应力(τ)为纵坐标,正应力(σn)是横坐标。经过最大和最小主应力的圆就是莫尔圆,因此,可以描述岩石的应力状态。破裂包络线将图分为稳定(黄色)和不稳定(灰色)区域。
破裂包络线的梯度是内摩擦角(φ),包络线与纵坐标在c点相交,即岩石的抗张强度。最大主应力和最小主应力均位于水平轴上。如果莫尔圆与破裂包络线相切,就会发生破裂,相对于最小主应力裂缝的方位是θ的两倍。
Terzaghi (1923)提出了对于饱和土的库伦破裂准则的修正,因为孔隙压力对降低有效应力具有重要的作用:
其中,\(P\)是孔隙压力。有效应力\(\sigma'_n=\sigma_n-P\)。
孔隙压力对破裂的影响#
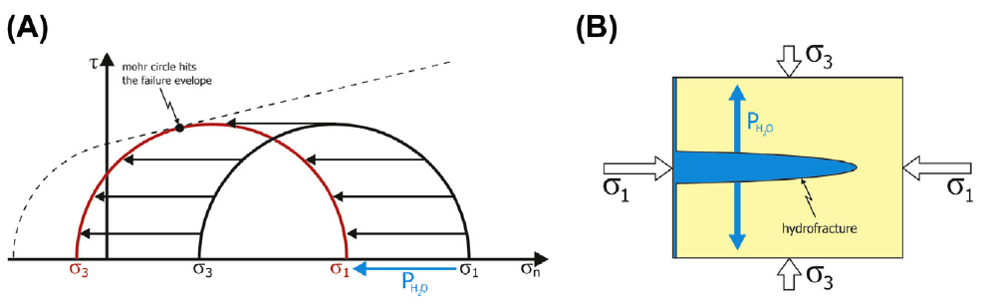
Hubbert and Rubey (1959)表明:岩石也应该考虑孔隙压力,正应力随着孔隙压力增加而减小。如图,莫尔圆在孔隙压力作用下向左移动。如果孔隙压力足够高,莫尔圆将一直左移直到与破裂包络线相交。在这一点上发生破裂。数学上,剪应力与正应力比值增加,因为孔隙流体压力降低了正应力。
孔隙压力是断裂作用机制的一个重要因素。以前的莫尔圆实例考虑了均质的、无裂缝的岩石发生破裂。为了允许沿着先存剪切破裂发生活动,Amonton定律描述了克服静摩擦力所需的剪切应力的大小,并表示为:
其中,\(\mu_s\)是静摩擦力,\(\sigma_n\)是垂直于裂缝面的作用力(Blau, 2013)。换句话说,超过在裂缝上滑动的力(即静摩擦力)与施加的正应力成正比。在预设裂缝的实例中,不需要考虑内聚力。